Sphere Class Reference

Class for Sphere objects. More...

#include <Sphere.h>

Inheritance diagram for Sphere:

Public Member Functions
	Sphere ()
	Sphere default constructor. More...
	Sphere (const Sphere &sphere)
	Sphere copy constructor. More...
	~Sphere ()
	Sphere destructor. More...
Sphere &	operator= (const Sphere &sphere)
	Sphere assignment operator. More...
std::vector< RayIntersection >	intersect (const Ray &ray) const
	Sphere-Ray intersection computation. More...

Additional Inherited Members
Public Attributes inherited from Object
Transform	transform
	A 3D transformation to apply to this Object. More...
Material	material
	The colour and reflectance properties of the Object. More...
Protected Member Functions inherited from Object
	Object ()
	Object default constructor. More...
	Object (const Object &object)
	Object copy constructor. More...
virtual	~Object ()
	Object destructor. More...
Object &	operator= (const Object &object)
	Object assignment operator. More...

Detailed Description

Class for Sphere objects.

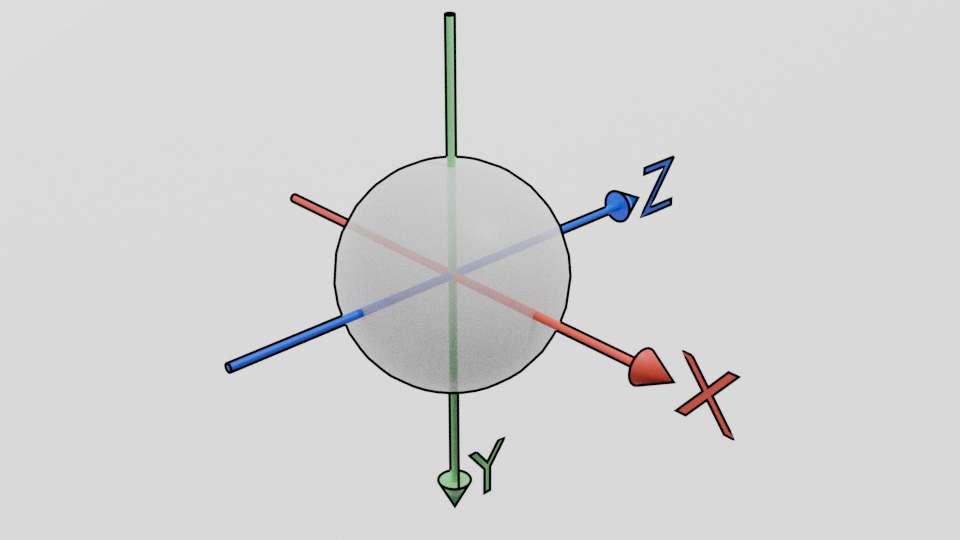
This class provides an Object which is a sphere centred at the origin with radius 1., as illustrated below:

Constructor & Destructor Documentation

Sphere() [1/2]

Sphere::Sphere

(

)

Sphere default constructor.

A newly constructed Sphere is centred at the origin, and has a raidus of 1. It may be moved, rotated, and scaled through its transform member.

Sphere() [2/2]

Sphere::Sphere

(

const Sphere &

sphere

)

Sphere copy constructor.

Parameters

sphere

The Sphere to copy.

~Sphere()

Sphere::~Sphere

(

)

Sphere destructor.

Member Function Documentation

intersect()

std::vector< RayIntersection > Sphere::intersect ( const Ray &  ray ) const

virtual

Sphere-Ray intersection computation.

The intersection of a Ray with a Sphere comes down to a quadratic formula of the form \(at^2 + bt + c\), where \(t\) is the distance along the Ray, and \(a\), \(b\), and \(c\) are some constants. The solutions for \(t\) are given by \($ \frac{-b \pm \sqrt{b^2-4ac}}{2a} \)$ The number of intersections depends on the value of \(b^2-4ac\). If it is negative then the Ray misses the Sphere and there are no intersections. A positive value indicates two intersection (entering and then leaving the Sphere). Finally, if \(b^2-4ac = 0\) then there is a single grazing hit with the Sphere.

Parameters

ray	The Ray to intersect with this Sphere.

Returns

A list (std::vector) of intersections, which may be empty.

Implements Object.

operator=()

Sphere & Sphere::operator=

(

const Sphere &

sphere

)

Sphere assignment operator.

Parameters

sphere

The Sphere to assign to this.

Returns

A reference to this to allow for chaining of assignment.

---

The documentation for this class was generated from the following files:

• Sphere.h
• Sphere.cpp