Class for Cylinder objects. More...
#include <Cylinder.h>
Public Member Functions | |
| Cylinder () | |
| Cylinder default constructor. More... | |
| Cylinder (const Cylinder &cylinder) | |
| Cylinder copy constructor. More... | |
| ~Cylinder () | |
| Cylinder destructor. More... | |
| Cylinder & | operator= (const Cylinder &cylinder) |
| Cylinder assignment operator. More... | |
| std::vector< RayIntersection > | intersect (const Ray &ray) const |
| Cylinder-Ray intersection computation. More... | |
Additional Inherited Members | |
 Public Attributes inherited from Object Public Attributes inherited from Object | |
| Transform | transform |
| A 3D transformation to apply to this Object. More... | |
| Material | material |
| The colour and reflectance properties of the Object. More... | |
 Protected Member Functions inherited from Object Protected Member Functions inherited from Object | |
| Object () | |
| Object default constructor. More... | |
| Object (const Object &object) | |
| Object copy constructor. More... | |
| virtual | ~Object () |
| Object destructor. More... | |
| Object & | operator= (const Object &object) |
| Object assignment operator. More... | |
Detailed Description
Class for Cylinder objects.
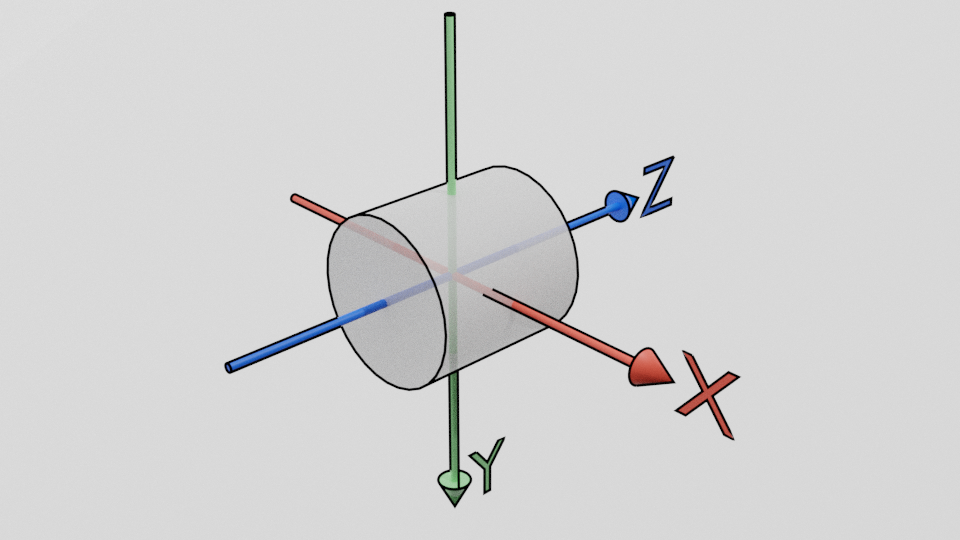
This class provides an Object which is a Cyclinder centred at the origin, with radius 1. The clyinder is aligned with the \(Z\)-axis, and extends to \( \pm 1\) along that axis, as illustrated below.
Note that the Cylinder provided in the skeleton code is not complete, and returns no RayIntersections from intersect(). This method needs to be implemented correctly as part of the assignment.
Constructor & Destructor Documentation
◆ Cylinder() [1/2]
| Cylinder::Cylinder | ( | ) |
◆ Cylinder() [2/2]
| Cylinder::Cylinder | ( | const Cylinder & | cylinder | ) |
◆ ~Cylinder()
| Cylinder::~Cylinder | ( | ) |
Cylinder destructor.
Member Function Documentation
◆ intersect()
|
virtual |
Cylinder-Ray intersection computation.
- Todo:
- The Cylinder-Ray intersection needs to be implemented as part of the assignment.
The intersection of a Cylinder and a Ray can be divided into three main parts:
- Intersections with the curved surface of the cylinder
- Intesections with the top cap (flat surface) of the cylinder
- Intesections with the bottom cap of the cylinder
Intersections with the curved surface are like the intersection with a Sphere, but the \(Z\)-axis can be ignored. You might think of this as intersecting a 2D ray in the \(X\)- \(Y\) plane with a unit circle. This leads to a quadratic equation, like that for the Sphere and 0, 1, or 2 hit points. These hit points would be with an 'infinite' cylinder extending along the \(Z\)-axis, so you should reject those with \(Z\) value greater than 1 or less than \(-1\).
The top cap can be seen as intersecting the Ray with the Plane \(Z=1\), so finding how far you need to go along the Ray to get a \(Z\) value of 1. Note that for some Rays this may never happen. Once you've found where the Ray intersects the plane \(Z=1\), check that the intersection is within 1 unit of the \(Z\)-axis.
The bottom cap is the same, except you are checking against the plane \(Z=-1\).
- Returns
- A list (std::vector) of intersections, which may be empty.
Implements Object.
◆ operator=()
The documentation for this class was generated from the following files: